原始帰納的関数

情報数学 理論計算機科学

• 原始再帰関数, Primitive Recursive Functionとも

定義 次の関数を原始帰納的関数という

• いくつかの決められた関数は原始帰納的関数である
  • 定数関数$zero:N^0\to N$, $zero()=0$
  • 後者関数$suc:N\to N$, $suc(x)=x+1$(xの次の数を返す)
  • 写影関数${\pi }_i^n:N^n\to N$, ${\pi }_i^n(x_1,x_2,...,x_n)=x_i$ (セレクタ)
• 原始帰納的関数の合成は原始帰納的関数である
  • $g:N^m\to N$と$h_i:N^n\to N(i=1,2,...,m)$が原始帰納的関数のとき、$f:N^n\to N,f(x_1,x_2,...,x_n)=g(h_1(x_1,x_2,...,x_n),...,h_m(x_1,x_2,...,x_n))$も原始帰納的関数である
• 原始帰納法による関数の定義
  • $g:N^n\to N$と$h:N^{n+2}\to N$が原始帰納的関数のとき、次のように定義した$f:N^{n+1}\to N$も原始帰納的関数である
    • $f(x_1,x_2,...,x_n,0)=g(x_1,x_2,...,x_n)$
    • $f(x_1,x_2,...,x_n,suc(y))=h(x_1,x_2,...,x_n,y,f(x_1,x_2,...,x_n,y))$

例

• イデアル関数: id(x) = x
• 定数関数: one() = 1
• add2(x) = suc(suc(x)) ←合成
• 2倍
  • インクリメント(suc)を2x回すればいい
  • double(0) = 0
  • double(suc(x)) = suc(suc(double(x)))
• 前者関数: pred(suc(y)) = y, pred(0) = 0
• 足し算
  • yの数だけ、xをインクリメント(suc)すればいい
  • add(x, suc(y)) = suc(add(x, y)), add(x, 0) = x
• 引き算
  • 足し算の逆
  • sub(x, 0) = x, sub(x, suc(y)) = pred(sub(x, y))
• 掛け算
  • mul(x, 0) = 0, mul(x, suc(y)) = add(x, mul(x, y))
• max:
  • max(x, y) = add(sub(x, y), x)
  • 別の方法
    • max(x, y) = tmp(x, y, sub(x, y)), tmp(x, y, 0) = y, tmp(x, y, d) = x

計算可能性

• 原始帰納的関数は計算可能
  • 証明
    • $zero,suc,{\pi }_i^n$は計算可能である
      • 計算可能であるということはフローチャートで書ける or whileで表現できるということだから、フローチャートを書いてあげればいい
        • フローチャートに起こせれば計算可能、ということの意味がよくわかってない(kekeho)
    • 原始帰納的関数の合成は計算可能である
      • $f(x_1,x_2,...,x_n)=g(h_1(x_1,x_2,...,x_n),...,h_m(x_1,x_2,...,x_n))$
      • これもフローチャートを書いてあげればいい
    • 原始帰納法は計算可能である
      • $f(x_1,x_2,...,x_n,0)=g(x_1,x_2,...,x_n)$
      • $f(x_1,x_2,...,x_n,suc(y))=h(x_1,x_2,...,x_n,y,f(x_1,x_2,...,x_n,y))$
      • これもフローチャートを書いてあげればいい その他
• for文に近い
• 原始帰納的関数 $\subset$ 計算可能関数 $\subset$ 関数
  • 原始帰納的関数は全域的関数(Total function)
    • 全域的: 入力に対して出力が必ずある
  • コンピュータが計算する関数は全域的関数とは限らない
    • 部分的関数であることもある
      • 部分的: 入力に対して出力がないこともある
      • 
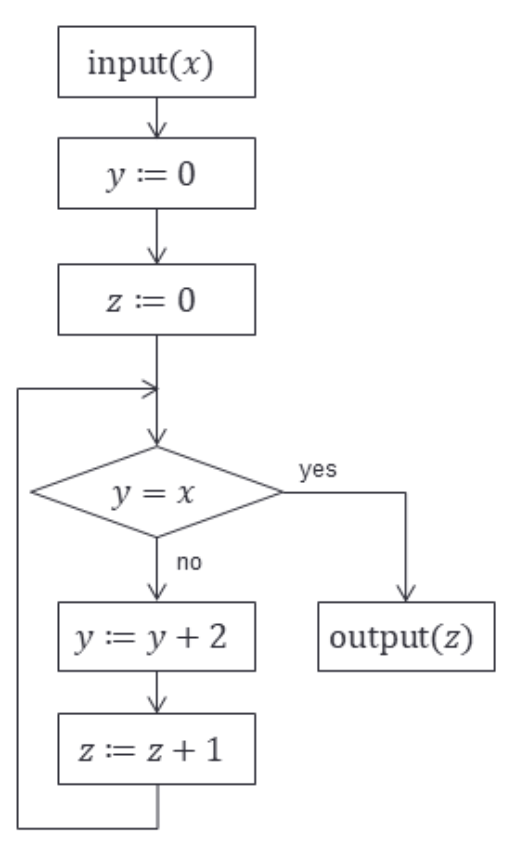
      • 奇数のときには止まらない
  • 全域的で計算可能だが、原始帰納的でない関数もある
    • アッカーマン関数 $A:N^2\to N$
      • $A(0,y)=suc(y)$
      • $A(suc(x),0)=A(x,suc(0))$
      • $A(suc(x),suc(y))=A(x,A(suc(x),y))$
    • 原始帰納的関数よりかなり計算量を食う

資料

• https://www.kurims.kyoto-u.ac.jp/~cs/lecture/2008/prf.pdf
• https://web.sfc.keio.ac.jp/~hagino/mi20/02.pdf