Merkle Search Tree

CRDT

論文 Merkle Search Trees Efficient State-Based CRDTs in Open Networks

• https://ieeexplore.ieee.org/document/9049566
• https://inria.hal.science/hal-02303490/document
• SRDS ‘2019

概要

• State-based CRDTの状態を[Merkle Search Tree]で表現すると、キーの順序を維持しながら分散イベントストアを作れる

  • 普通の2分木のMerkle Treeでは、木がうまくバランスするようにする再構築の過程で順序が破壊されるので、うまくいかない
  • Vector Clock(Logical Clock)を使う方法では、線形に増えていってしまうので厳しい MSTのデータ構造

• 特徴

  • アイテムの集合は、決定論的に一意な木の表現を持つ
  • キーの順序は保持される
  • ツリーは常にバランスが取れている(確率的) ←どういうこと?(kekeho)

• Merkle Search Treeの構成

  • MSTは、全順序の空間$\mathbb{K}$に含まれる要素$e$の順序付き集合を作る
    • 例: 連想配列
      • 要素は、$\mathbb{V}$(値)に紐付けられたタグとなる。$\mathbb{K}$はキーの集合
      • $\mathbb{V}$はデフォルト要素の$\perp$を持つ。$f:\mathbb{K}\to \mathbb{V}$にキーが存在しないことを示すために用いられる。
    • 予め、$e\in \mathbb{K}$の順序が決定的に決まっているからできる。例えば、挿入時に順序付けをするような場合では一筋縄ではいかないんだろう(kekeho)

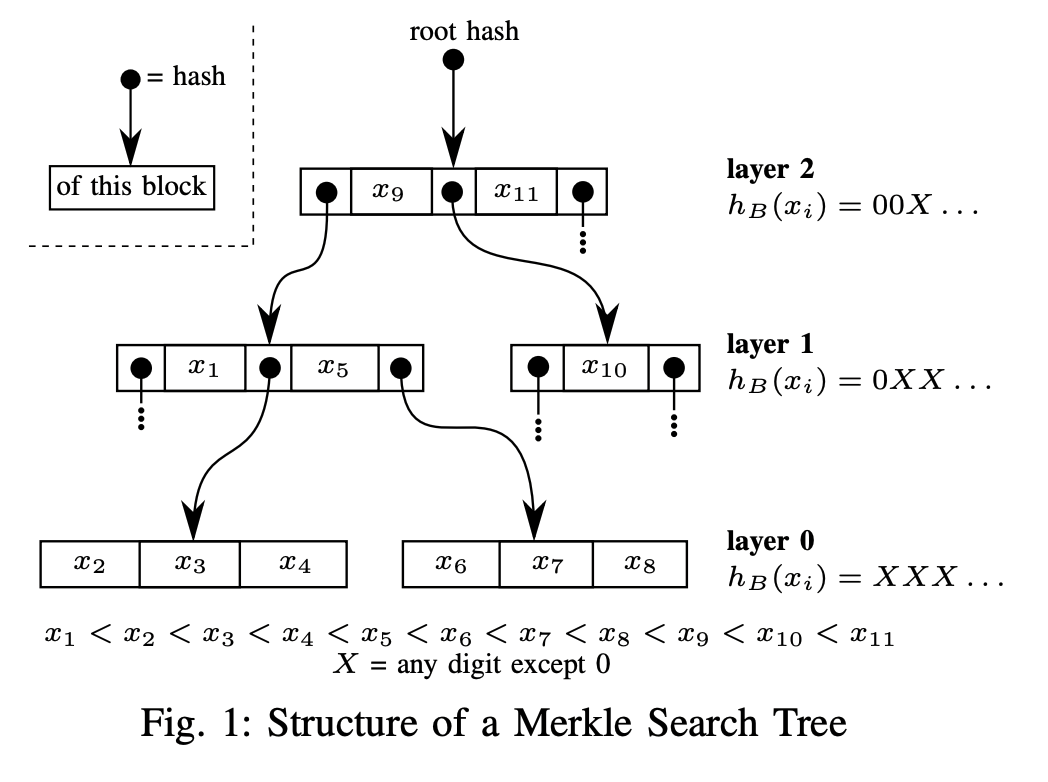
• B-TreeライクなSearch Treeを作る(Fig. 1)

  • Leafがレイヤ0
  • レイヤ$l$にいるノードたちは、連続するアイテムのブロックであり、その境界は$l^{\prime }>l$のアイテムに対応する
  • MSTに格納される値は、そのハッシュを計算し、その値をベースレイヤに書き込む
    • 書き込むレイヤ$l(x)$は、$h_B(x)$のゼロのみで構成される最長の接頭辞の長さで決定される
    • $h_B$: Digestの空間サイズが$2^B$となるようなハッシュ関数
      • SHA512ならBが512ということなんだと思う(kekeho)
  • ポインタとして下レイヤのハッシュを書く
  • 先頭ビットの0の数でレイヤを測る
  • 各ノードのサイズは一定のサイズを持たない(普通のB-Treeはページサイズとかがあったはず?(kekeho))

• 操作の定義

  • MSTをKVSとして扱うときの例
    • $\mathrm{get}(f,k)$: ツリー$f$からキー$k$に対応する値を読み取る
    • $\mathrm{getrange}(f,[k_0,k_1])$: ツリー$f$からキー範囲が$k_0$ ~ $k_1$に含まれる値の集合を読み取る
    • $\mathrm{put}(f,k,v)$: ツリー$f$のキー$k$に値$v$を書き込む
    • $\mathrm{delete}(f,k)$: ツリー$f$からキー$k$を消す
  • 非リーフ層で値の追加・削除が発生すると、Split・Mergeが発生する可能性がある。

• バランスと深さ

  • あるアイテムがレイヤ$l$にある確率は$p_l=(\frac{1}{B}{)}^l\frac{B-1}{B}$
  • レイヤ$l$のアイテム数は、レイヤ$l^{\prime }>l$の境界でSplitされるので、レイヤ$l$のノードは平均$B-1$個の値が格納され、リーフでない層は$B$個のノードを持つ

• データセット比較の効率性

• Merkle Search Trees as CRDT

  • $\mathbb{V}$がCRDTであり、マージ操作${\bigsqcup }_{\mathbb{V}}$( $\forall x,\perp {\bigsqcup }_{\mathbb{V}}x=x{\bigsqcup }_{\mathbb{V}}\perp =x$)を持つ
    • 具体的にマージ操作をどう定義すればいいんだ? (kekeho)
  • さすれば、$\bigsqcup \mathrm{v}:(f\bigsqcup g)(x)=f(x)\bigsqcup \mathrm{v}g(x)$で定義されるMST$f,g:\mathbb{K}\to \mathbb{V}$はCRDTとなる
  • 例: $\mathbb{K}$のG-set
    • $\mathbb{V}=\{\perp ,\mathsf{T}\}$とすれば、OK
    • たしかにねー(kekeho)

アルゴリズム

• MSTはPersistent Data Structuresなので、分散MSTの構築もできる

アプリケーション: 分散イベントストア

• $\mathbb{V}=T,F$
• $\mathbb{K}$: イベント空間(Logical Clock or 実時間の近似値で並べられる)