イェンセンの不等式

• 簡潔データ構造のサイズの上界(Upper-bound)を求める際に用いられる
  • 空間計算量

凸関数の定義

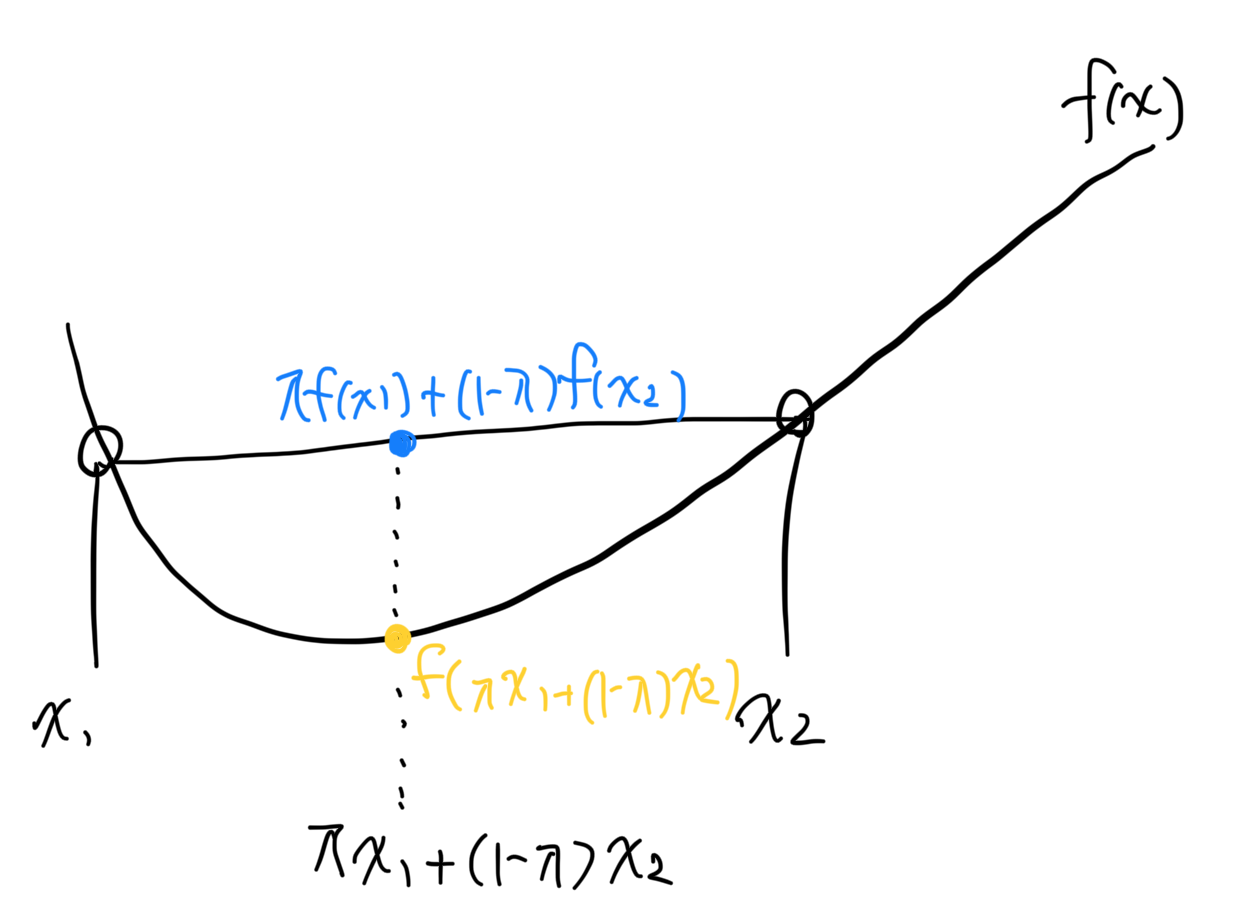
• 任意の$x_1,x_2\in I$と$0\le \lambda \le 1$について、以下の不等式を満たすとき$f$を下に凸関数と呼ぶ
  • $f(\lambda x_1+(1-\lambda )x_2)\le \lambda f(x_1)+(1-\lambda )f(x_2)$
  • $x_1\le \lambda x_1+(1-\lambda )x_2\le x_2$、$f(x_1)\le \lambda f(x_1)+(1-\lambda )f(x_2)\le f(x_2)$であることに注意
• 狭義凸関数の定義: 任意の$x_1,x_2\in I(x_1\ne x_2)$と$0<\lambda <1$について以下の不等式を満たすとき$f$を下に狭義凸関数と呼ぶ
  • $f(\lambda x_1+(1-\lambda )x_2)<\lambda f(x_1)+(1-\lambda )f(x_2)$
  • 例: $x^2,logx,e^x...$
    • $f(x)$が定義されているところに、フラットなところ、直線的なところがなにもないイメージ

イェンセンの不等式

• 凸関数の定義の一般化
• $f(x)$が下に凸の関数で、$x_1,x_2,...,x_n\in I,{\lambda }_1,...,{\lambda }_n$を${\sum }_{k=1}^n{\lambda }_k=1$かつ${\lambda }_k\ge 0$とする。このとき、次のような不等式が成り立つ。
  • ${\sum }_{k=1}^n{\lambda }_{k}f(x_k)\ge f({\sum }_{k=1}^n{\lambda }_k{x}_k)$